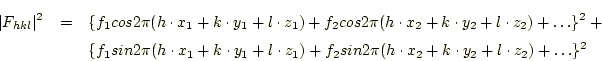

Next: 課題レポート02の内容
Previous: コンピュータ演習課題レポート02 問題
波長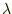 のX線を結晶に入射した場合、面間隔
のX線を結晶に入射した場合、面間隔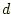 を有する結晶面とX線の回折角
を有する結晶面とX線の回折角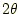 には以下の関係がある。
には以下の関係がある。
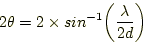 |
(1) |
ただし、
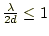 でなくてはならない。
でなくてはならない。
このとき、任意の(hkl)面のX線回折強度 は構造因子
は構造因子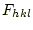 を用いて、
を用いて、
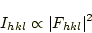 |
(2) |
と表される。ここに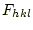 は、
は、
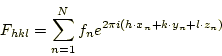 |
(3) |
であり、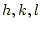 は面指数、
は面指数、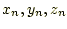 はn番目の原子の部分座標、
はn番目の原子の部分座標、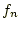 はn番目の原子のX線散乱能である。オイラーの公式(
はn番目の原子のX線散乱能である。オイラーの公式(
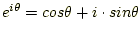 )から、上式は以下のようにも記述できる。
)から、上式は以下のようにも記述できる。
![\begin{displaymath}
F_{hkl} = \sum_{n = 1}^N f_n [cos 2\pi (h \cdot x_n + k \cdo...
... + i \cdot sin 2\pi (h \cdot x_n + k \cdot y_n + l \cdot z_n)]
\end{displaymath}](img14.png) |
(4) |
従って、
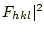 は、
は、
と実数の三角関数のみを用いて表現できる。


Next: 課題レポート02の内容
Previous: コンピュータ演習課題レポート02 問題
Hitoshi Takamura
平成16年11月5日
![]() は構造因子
は構造因子![]() を用いて、
を用いて、
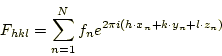
![\begin{displaymath}
F_{hkl} = \sum_{n = 1}^N f_n [cos 2\pi (h \cdot x_n + k \cdo...
... + i \cdot sin 2\pi (h \cdot x_n + k \cdot y_n + l \cdot z_n)]
\end{displaymath}](img14.png)