コンピュータ演習課題レポート02　問題

（提出〆切：平成15年11月7日（金）13：00）

１）面間隔dからX線回折計の回折角2θを計算する方法

　　　　　

　　　　　　　　　　　 　　　　 • • • (1)

　　　　　 ただし、　でなくてはならない。

　

２）任意の結晶の(hkl)面のX線回折強度を計算する方法

　任意の結晶の(hkl)面のX線回折強度は、構造因子を用いて、

　　　　　　　　　　　　　　　　　 　　　　 　　　　　 • • • (2)

と表される。ここには、

　　　　　　　　　　　　　　　　　 　　　　　 　• • • (3)

である。は以下の様にも記述できるので、

　　　　　　　　　　　　　　　　　 　　　　 • • • (4)

従って、は、

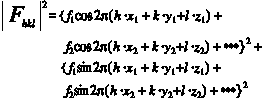　　　　　　　　　　　 　　　 • • • (5)

と実数の三角関数のみを用いて表現できる。

３）課題レポートの内容

　ここで、前回作成した(hkl)面の面間隔を計算するプログラムを改良して、以下のように、実際に六方晶構造を有するMgの各面指数(hkl)について、面間隔d(nm)、回折角2θ (°)、およびを計算し出力するプログラムを作成し提出せよ。

ただし、

a) 六方晶構造を有するMgの場合、面間隔d、格子定数a,c、面指数h, k, lの間には次式の関係がある：

b) Mgの結晶構造に関するデータ：

格子定数：　 a = 0.3209 (nm)

c = 0.5211 (nm)

単位格子に含まれるMg原子数： n = 2

その二つの Mg原子の部分座標： (0, 0, 0),　 (0.6667, 0.3333, 0.5)

であり、この課題においては、 =　 1と仮定してよい。

c) X線の波長は0.15405(nm)を用いよ。

d) の値が、0.001より大きい面についてのみ出力すること。

e) 2θが180°を超えないこと。

f) h, k, lの範囲は-4〜+4とする。

g) 出力を2θの小さい順にUNIXのsortコマンドを利用して並べかえること。（先週のページ参照）

出力例（実際は286行）

( 0 1 0 ) d = 0.2779 nm 2Theta = 32.18 F_square = 1.00e+00
( 0 -1 0 ) d = 0.2779 nm 2Theta = 32.18 F_square = 1.00e+00
( 1 0 0 ) d = 0.2779 nm 2Theta = 32.18 F_square = 1.00e+00
ーーー途中は省略ーーー
( 3 1 0 ) d = 0.0771 nm 2Theta = 175.76 F_square = 9.99e-01
( -1 -3 0 ) d = 0.0771 nm 2Theta = 175.76 F_square = 9.99e-01
( -3 -1 0 ) d = 0.0771 nm 2Theta = 175.76 F_square = 9.99e-01

４）注意事項

a) 数学関数・定数を利用するので、#include<math.h>を忘れない。

b) 数学関数を利用するので、コンパイル時に-lmをつけるのを忘れない。

c) 円周率はM_PIという定数を利用することができる。

d) （）はasin()という関数を利用する。

e) asin()が返す角度の単位はラジアン：asin(1)= /2 =1.5707...

f) UNIXのsortコマンド：sort -k [ソートの対象列番号]

g) 提出後、必ず、execution_resultを確認すること。

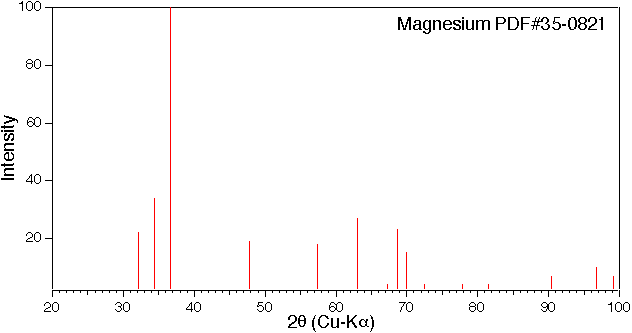
実際に粉末回折図形のデータベース（JCPDS）に登録されいてるパターンはこちら