配列：同類のデータをひとまとまりに扱うための入物

1. 宣言方法
   
   int a[100];
   

   この宣言により、a[0], a[1], a[2], ..., a[99] の100個の整数型の変数を用意することができる。 (各々の要素に任意の整数を代入することが可能)

   	a[0] = 12345;
   	a[1] =  6789;
   

   
   
2. メリット
   

   for文や、while文などにより一括してデータを扱うことが可能

   	sum = 0;
   	for (i = 0; i < 100; ++i) sum = sum + a[ i ];
   

   
   
3. 使用上の注意点
   
   • あらかじめ配列の大きさを決定する必要があり、不用意に大きな配列を宣言すると、コンパイル時、実行時に多くのメモリを消費する。（解決方法：動的な変数の確保）
   • 型の違う変数をひとまとまりの配列にはできない。 （解決方法：構造体の利用）
   
   
4. 使用例
   
   
   • 宣言時の初期値の与え方：

     	int  a[5] = {0, 1, 2, 3, 4};
     

     
     
   • for文による配列の初期化：

     	for(i=0; i<5; ++i){ a[i] = 0; }
     

     
     
   • 配列の利用例(n!を配列に代入し、表示するプログラム)：

     #include <stdio.h>
     main(){
     int i, j, c[5];
     	for(i=0; i<5; ++i){ c[i] = 1; }
     	for(i=0; i<5; ++i){
     		for(j = 1; j <= i; ++j){
     			c[i] = c[i]*j;
     		}
     	}
     	for(i=0; i<5; ++i){ printf("c[%d]= %d! = %d\n", i, i, c[i] ); }
     }

     
     
   • 多次元配列
     

     	int two_dimension[100][100];
     	100行×100列の配列
     

5. 練習問題１：前回の課題レポートでは、Mg原子の部分座標、（0,0,0）と（0.6667,0.3333,0.5）、を構造因子の二乗F*Fを計算する式中に直接代入していた。 しかし、このプログラムを他の結晶 のX線回折図形の計算に利用できるようにするためには、この部分を一般化する方が良い。 そこで、原子の部分座標を記憶する2次元配列atom[2][3]を用意し、以下の仕様に変更せよ。
   • 2個の原子座標（x, y, z）格納できる配列atom[2][3]を用意する。
   • プログラム中において、原子の部分座標を以下のように配列に代入する
     atom[0][0] = 0.0 ;
     atom[0][1] = 0.0 ;
     atom[0][2] = 0.0 ;
     atom[1][0] = 0.3333 ;
     atom[1][1] = 0.6667 ;
     atom[1][2] = 0.5;
     
   • for文を利用して配列の部分座標をF*Fを計算する式に取込み、前回と同じ計算結果を得るプログラムを作成せよ。
     
     
6. 練習問題2：上の問題では、格子定数、原子座標をプログラム中に記述している。さらに、利便性を高めるために、これらの情報（格子定数、単位胞中に含まれる原子数、原子座標）をscanf文を利用して実行時に入力できるように改良せよ。また、その際、これまで１と仮定していた原子のＸ線散乱能を各原子の原子番号として、原子座標と同時に入力できるように配列を１列増やすこと。そのプログラムを用いて、以下の水素吸蔵合金として有名なLaNi₅の粉末X線回折パターンを計算してみよ。その結晶に関する情報は以下の通り。
   • 格子定数：a = 0.5015 nm, c = 0.3984
   • 単位胞中に含まれる原子数：6
   • 原子座標(x , y, z)と原子番号(f)：
     1. (0, 0, 0, 57)
     2. (0.33333, 0.66667, 0, 28)
     3. (0.66667, 0.33333, 0, 28)
     4. (0.5, 0, 0.5, 28)
     5. (0, 0.5, 0.5, 28)
     6. (0.5, 0.5, 0.5, 28)
     
     
   • 実行画面：（下線部はキーボードからの入力）
     Lattice constant a, c (nm) = 0.5015 0.3984
     The number of atoms in the unit cell = 6
     No. 0 (x, y, z, f) = 0 0 0 57
     No. 1 (x, y, z, f) = 0.33333 0.66667 0 28
     No. 2 (x, y, z, f) = 0.66667 0.33333 0 28
     No. 3 (x, y, z, f) = 0.5 0 0.5 28
     No. 4 (x, y, z, f) = 0 0.5 0.5 28
     No. 5 (x, y, z, f) = 0.5 0.5 0.5 28
     
     実行結果：（５９０行の内の最初の１０行）
     ( -4 -2 -1 ) d = 0.0804 nm 2Theta = 146.73 F_square = 2.44e+03
     ( -4 -2 0 ) d = 0.0821 nm 2Theta = 139.58 F_square = 2.44e+03
     ( -4 -2 1 ) d = 0.0804 nm 2Theta = 146.73 F_square = 2.44e+03
     ( -4 -1 -3 ) d = 0.0771 nm 2Theta = 173.64 F_square = 7.22e+03
     ( -4 -1 -2 ) d = 0.0856 nm 2Theta = 128.32 F_square = 7.22e+03
     ( -4 -1 -1 ) d = 0.0922 nm 2Theta = 113.31 F_square = 7.22e+03
     ( -4 -1 0 ) d = 0.0948 nm 2Theta = 108.72 F_square = 7.22e+03
     ( -4 -1 1 ) d = 0.0922 nm 2Theta = 113.31 F_square = 7.22e+03
     ( -4 -1 2 ) d = 0.0856 nm 2Theta = 128.32 F_square = 7.22e+03
     ( -4 -1 3 ) d = 0.0771 nm 2Theta = 173.64 F_square = 7.22e+03
     
     
   • さらに、以下のファイルをあらかじめ用意しておくことにより、UNIXのリダイレクトを利用して結晶に関するデータをキー入力なしに実行プログラムに引き渡すことが可能。
     
     
     • 用意するテキストファイル（以下の内容を例えばlani5.txtとして保存する）
       0.5015 0.3984
       6
       0 0 0 57
       0.33333 0.66667 0 28
       0.66667 0.33333 0 28
       0.5 0 0.5 28
       0 0.5 0.5 28
       0.5 0.5 0.5 28
       
       
     • リダイレクトの使い方
       実行プログラム名 < 入力ファイル名 > 出力ファイル名
       もし、実行ファイル名がa.out、データのテキストファイル名がlani5.txt、結果を出力するファイル名をoutputとするならば、
       a.out < lani5.txt > output
       となる。この場合、プログラムでファイルの入出力（fopen文やfscanf文、fprintf文）を利用する必要はないことに注意。
       
       
7. ポインタについて（変数はどこに記憶されるのか？）
   
   以下のプログラム(pointer.c)を作成し、実行してみよ。
   
   
   

   &を変数の前につける：変数が格納されている番地（アドレス）を示す

   *をアドレスの前につける：そのアドレスに格納されている値を示す

   
   
8. pointer.cの解説
   
   
   
   
9. 以下のプログラム（pointer2.c）を作成し、ポインタ変数の挙動について考えよ。

   #include 
   main()
   {
     int a = 100, b = 200, *pa, *pb;
     pa = &a; pb = &b;
     printf("a = %d, pa = %x, *pa = %d\n", a, pa, *pa);
     printf("b = %d, pb = %x, *pb = %d\n", b, pb, *pb);
   }
   

   
   
   
   • ポインタ変数 ＝ 変数のアドレスを記憶するための変数
   • 変数定義部の＊とprintf中の＊の意味の違いに注意
   
   さらに、ポインタ変数(*pa)のポインタ変数(**ppa)を用いた以下のプログラムを入力し、ポインタ変数への理解を深めよ。最後のprintf文中の下線部において、ポインタ変数ppaを用いてaの値100を表示するためにはppaの前に何をつければよいか考えよ。
   
   
   
   
10. 配列とポインタの関係
    

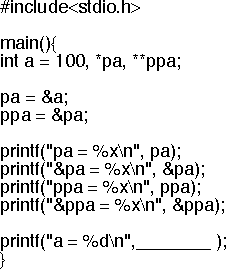
    →配列名自身は、配列の先頭アドレスを有する

    
    以下のプログラム(array.c)を作成し、実行せよ。
    

    #include 
    main()
    {
      int i, a[10] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
      for(i = 0; i < 10; ++i){
        printf("a[%d]=%d a+%d=%x *(a+%d)=%d\n",
    			i, a[i] , i, a+i, i, *(a+i));
      }
    }
    
    実行結果
    a[0]=0 a+0=effffa00 *(a+0)=0
    a[1]=1 a+1=effffa04 *(a+1)=1
    a[2]=2 a+2=effffa08 *(a+2)=2