- Solve[x^2 - 1 == 0, x]
- Solve[x^2 + 1 == 0, x]
- D[Sin[x], x]
- Integrate[Sin[x], x]
- Limit[Sin[x]/x, x-> 0]
- Solve[x - Exp[-x] + Sin[x] == 0, x]
- 二分法
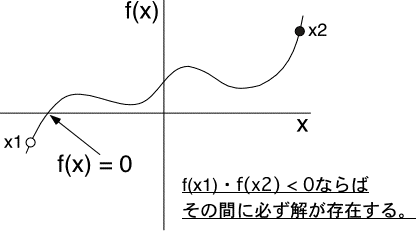
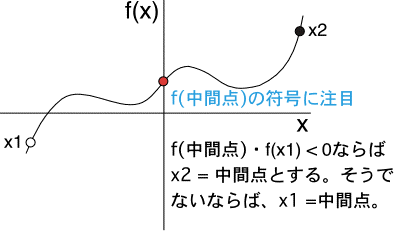
この計算・判定を繰り返して(x1-x2)の絶対値がある値以下(例えば、1.0E-6等)になれば、(x1+x2)/2が確からしい解と推定される。 この考え方を用いて、下記の関数の解を数値的に求めてみよ。
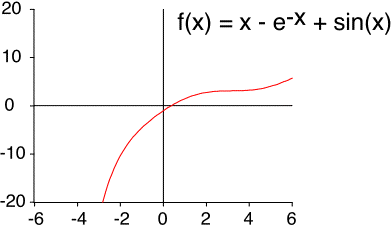
以下にヒントを示す。
#include<stdio.h> #include<math.h> #define MAXNUM 1000 ← 繰り返しの最大数 #define EPS 1.e-6 ← 収束判定の基準(x1-x2の絶対値がこれより小さくなったら計算終了) double f(double x) ← 今問題としている関数 { return(x - exp(-x) + sin(x)); } main() { double x1, x2, mid_x; ← 挟み込む変数x1, x2と中間点mid_x int i; x1 = -100.0; ← x1の初期値 x2 = 100.0; ← x2の初期値 for(i = 0; i < MAXNUM; ++i){ ここを考えてみよう! if(fabs(x1 - x2) < EPS){ ← ここで用いている組み込み数学関数fabs()は実数の絶対値を与える printf("Ans. = %lf (Iteration No. = %d)\n", (x1+x2)/2, i); break; } } } 以下に実行結果例を示す。 There should be an answer! (x1 = -100.000000 x2 = 100.000000) There should be an answer! (x1 = 0.000000 x2 = 100.000000) There should be an answer! (x1 = 0.000000 x2 = 50.000000) There should be an answer! (x1 = 0.000000 x2 = 25.000000) There should be an answer! (x1 = 0.000000 x2 = 12.500000) There should be an answer! (x1 = 0.000000 x2 = 6.250000) There should be an answer! (x1 = 0.000000 x2 = 3.125000) There should be an answer! (x1 = 0.000000 x2 = 1.562500) There should be an answer! (x1 = 0.000000 x2 = 0.781250) There should be an answer! (x1 = 0.000000 x2 = 0.390625) There should be an answer! (x1 = 0.195312 x2 = 0.390625) There should be an answer! (x1 = 0.292969 x2 = 0.390625) There should be an answer! (x1 = 0.341797 x2 = 0.390625) There should be an answer! (x1 = 0.341797 x2 = 0.366211) There should be an answer! (x1 = 0.354004 x2 = 0.366211) There should be an answer! (x1 = 0.354004 x2 = 0.360107) There should be an answer! (x1 = 0.354004 x2 = 0.357056) There should be an answer! (x1 = 0.354004 x2 = 0.355530) There should be an answer! (x1 = 0.354004 x2 = 0.354767) There should be an answer! (x1 = 0.354385 x2 = 0.354767) There should be an answer! (x1 = 0.354385 x2 = 0.354576) There should be an answer! (x1 = 0.354385 x2 = 0.354481) There should be an answer! (x1 = 0.354433 x2 = 0.354481) There should be an answer! (x1 = 0.354457 x2 = 0.354481) There should be an answer! (x1 = 0.354457 x2 = 0.354469) There should be an answer! (x1 = 0.354463 x2 = 0.354469) There should be an answer! (x1 = 0.354463 x2 = 0.354466) There should be an answer! (x1 = 0.354463 x2 = 0.354464) Ans. = 0.354463 (Iteration No. = 27)
電卓等を用いて、実際に求められた値を用いてf(x)がゼロに限りなく近いことを確認せよ。ここで注目すべきことは、全繰り返し数(27回)の内、13回程度は0.35まで求められた後に精度を上げるために費やされている点。解答例はこちら。
- Newton-Raphson法
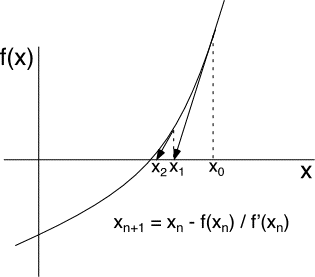
計算を高速化するためにNewton-Raphson法を用いてみよう。この方法では、上図のようにある初期値(x0)から出発して、まずf(x0)を求める。その点において、対象の関数の微分を利用して新しいx1を求める。この計算を繰り返し、二分法と同様に、(xn+1-xn)の絶対値がある値以下(例えば、1.0E-6等)になればxn+1が解と推定される。このアルゴリズムを用いて先ほどの関数f(x) = x - exp(-x) + sin(x)の解を探してみよ。なお、その際初期値(x0) は-10程度とせよ。解答例はこちら。
実行例:x1 = -10.000000 f(x) = -2.203592e+04 x1 = -8.999578 f(x) = -8.109077e+03 x1 = -7.998427 f(x) = -2.985261e+03 x1 = -6.995696 f(x) = -1.099572e+03 x1 = -5.990308 f(x) = -4.052391e+02 x1 = -4.980982 f(x) = -1.496341e+02 x1 = -3.962250 f(x) = -5.580612e+01 x1 = -2.907188 f(x) = -2.144471e+01 x1 = -1.737430 f(x) = -8.406301e+00 x1 = -0.447499 f(x) = -2.444605e+00 x1 = 0.257826 f(x) = -2.599237e-01 x1 = 0.352700 f(x) = -4.654511e-03 x1 = 0.354462 f(x) = -1.627854e-06 Ans. = 0.354463 (Iteration No. = 12)
二分法に比較して、高速に収束している様子が分かる。特に、解の近傍での収束の程度に着目。
つぎに同じプログラムを初期値を100として実行してみよ。
実行例:x1 = 100.000000 f(x) = 9.949363e+01 x1 = 46.575403 f(x) = 4.709680e+01 x1 = -274.498393 f(x) = -1.633568e+119 x1 = -273.498393 f(x) = -6.009560e+118 x1 = -272.498393 f(x) = -2.210794e+118 x1 = -271.498393 f(x) = -8.133055e+117 x1 = -270.498393 f(x) = -2.991984e+117 途中を大幅に省略。 x1 = -11.498324 f(x) = -9.856109e+04 x1 = -10.498231 f(x) = -3.626095e+04 x1 = -9.497980 f(x) = -1.334220e+04 x1 = -8.497274 f(x) = -4.910685e+03 x1 = -7.495459 f(x) = -1.808282e+03 x1 = -6.491527 f(x) = -6.662283e+02 x1 = -5.484392 f(x) = -2.456703e+02 x1 = -4.471736 f(x) = -9.100908e+01 x1 = -3.440708 f(x) = -3.435507e+01 x1 = -2.341467 f(x) = -1.345538e+01 x1 = -1.083937 f(x) = -4.924040e+00 x1 = 0.029054 f(x) = -9.132590e-01 x1 = 0.336452 f(x) = -4.770932e-02 x1 = 0.354399 f(x) = -1.684415e-04 x1 = 0.354463 f(x) = -2.135317e-09 Ans. = 0.354463 (Iteration No. = 279)
今回は収束に至るに279回もの繰り返し計算を行っている。この原因について考察してみよ。
上の例で示されたように、二分法、Newton-Raphson法ともに長所・短所を有している。そこで、両者の長所をいかし、計算の最初においては二分法を用い、xn - xn+1の絶対値が1程度となったらNewton-Raphson法へ移行するプログラムを作成しxstudentから提出せよ。ただし、
- 方程式:x - exp(-x) + sin(x) = 0
- 2つの初期値は、100と-100とする。
- 答えだけではなく収束の過程も表示すること。
- xstudentからの提出においてはソースファイルのみではなく、コンパイルの命令、実行命令を入力すること。
- さらに、提出後かならずexecution_result.logの中に意図した結果が含まれているかを確認すること。
実行例:
There should be an answer between x1 = -100.000000 and x2 = 100.000000. There should be an answer between x1 = 0.000000 and x2 = 100.000000. There should be an answer between x1 = 0.000000 and x2 = 50.000000. There should be an answer between x1 = 0.000000 and x2 = 25.000000. There should be an answer between x1 = 0.000000 and x2 = 12.500000. There should be an answer between x1 = 0.000000 and x2 = 6.250000. There should be an answer between x1 = 0.000000 and x2 = 3.125000. There should be an answer between x1 = 0.000000 and x2 = 1.562500. OK, now let's use the Newton-Raphson method. x1 = 0.000000 f(x) = -1.000000e+00 x1 = 0.333333 f(x) = -5.600328e-02 x1 = 0.354375 f(x) = -2.314229e-04 x1 = 0.354463 f(x) = -4.030575e-09 Ans. = 0.354463