Next: 粉末X線回折による解析例 Up: X線回折法の結晶構造解析への応用 Previous: X線の発生
X線回折法の実際の応用例として粉末試料のディフラクトメータによる測定について述べる。ディフラクトメータは、図5.6に示すように、独立に回転する回転軸を有する精密測定機の一つである。これらの回転軸を慣習としてそれぞれ![]() 軸および2
軸および2![]() 軸と呼ぶ。通常にはω軸には粉末試料がセットされた平板状の試料ホルダーが取り付けられ、2
軸と呼ぶ。通常にはω軸には粉末試料がセットされた平板状の試料ホルダーが取り付けられ、2![]() 軸には散乱X線強度測定用のカウンターが取り付けてある。これらの軸は、入射X線の透過の方向を0
軸には散乱X線強度測定用のカウンターが取り付けてある。これらの軸は、入射X線の透過の方向を0![]() として、それぞれ
として、それぞれ![]() 軸が
軸が![]() 回転すると、2
回転すると、2![]() 軸は2
軸は2![]() 回転するように設計されている。
回転するように設計されている。
粉末結晶試料における回折強度の一般式は、
で与えられる。ここで、![]() は構造因子、
は構造因子、![]() は多重度因子、次の括弧内の因子はローレンツ偏光因子である。
は多重度因子、次の括弧内の因子はローレンツ偏光因子である。
![]() は吸収因子であるが、試料が十分厚いときには散乱角に依存せず一定値となる。またデバイ-ワーラー因子
は吸収因子であるが、試料が十分厚いときには散乱角に依存せず一定値となる。またデバイ-ワーラー因子![]() は、X線の原子散乱因子に影響するが、通常の相対強度の算出では省略することが多い。したがって、式(5.1)に基づいて、対象となる粉末X線結晶試料の回折ピークの相対強度を定量的に見積もることができる。各項についてのより詳しい説明を以下に記す。
は、X線の原子散乱因子に影響するが、通常の相対強度の算出では省略することが多い。したがって、式(5.1)に基づいて、対象となる粉末X線結晶試料の回折ピークの相対強度を定量的に見積もることができる。各項についてのより詳しい説明を以下に記す。
構造解析を行う際に、測定データと計算値を比較する上で最も基本となる因子であり、![]() 反射に対して、
反射に対して、
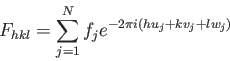
で与えられる。ここで、![]() は単位胞内のj番目の原子の原子散乱因子、
は単位胞内のj番目の原子の原子散乱因子、![]() は
は![]() 番目の原子位置を格子定数を単位として表した座標、
番目の原子位置を格子定数を単位として表した座標、![]() は単位胞内の原子の数である。
は単位胞内の原子の数である。
試料によって回折されたX線の強度は、観測する方向に垂直な面への入射X線の振幅の投影を考え、その2乗で表すことができる。偏光因子は、この投影成分と強度の関係から求めることができる。
面間隔が同じでかつ同じ構造因子を示すが、方位の異なる結晶面の数を表す。たとえば、立方晶の{100}の多重度因子は、![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() となり6である。
となり6である。
Hitoshi TAKAMURA