

Next: 積分過程(分子動力学シミュレーションの本体部分)
Previous: 相関距離の計算
今回の問題では、以下のレナード・ジョーンズ型ポテンシャルが粒子間に作用すると仮定しています。
粒子i, j間に作用する力
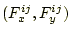 は
は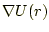 なので
なので
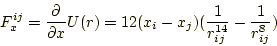 |
(4) |
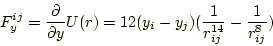 |
(5) |
となります。なお、このときポテンシャル中の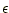 と
と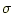 は1に規格化されています。この式を用いて以下の手順で各粒子が受ける力を計算します。
は1に規格化されています。この式を用いて以下の手順で各粒子が受ける力を計算します。
- 配列force[200][2]を用意する。型に注意。また、配列の長さは粒子の数と同じで次元は2(x, y方向の力を格納)である。
- 配列を0で初期化する。
- 以下のプロセスをペアリストの数だけ繰り返す。
- ペアリストから粒子番号(i, j)を抽出する。
- 力の作用する範囲
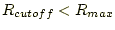 にある場合だけ力を計算する。例えば、
にある場合だけ力を計算する。例えば、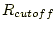 = 2.5。
= 2.5。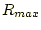 内の粒子全てを考慮しない理由を考えてみよ。
内の粒子全てを考慮しない理由を考えてみよ。
- 一方の粒子iに作用する力
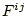 は座標値の差
は座標値の差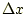 と距離
と距離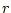 から計算できる。
から計算できる。
- 他方の粒子jには反作用の力
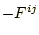 が作用する。
が作用する。
- それぞれの力を該当する粒子の配列forceに足していく。例えばx方向であればforce[i][0]とforce[j][0]に、y方向であればforce[i][1]とforce[j][1]に加えていく。
ペアリストの数だけ力を足していくプロセスが完了すれば、各粒子に働く力が配列forceに格納されている。以上の内容も関数として実装します。


Next: 積分過程(分子動力学シミュレーションの本体部分)
Previous: 相関距離の計算
Hitoshi Takamura
平成16年12月26日
![]() と
と![]() は1に規格化されています。この式を用いて以下の手順で各粒子が受ける力を計算します。
は1に規格化されています。この式を用いて以下の手順で各粒子が受ける力を計算します。