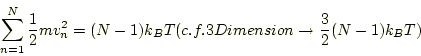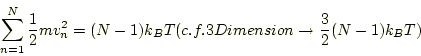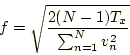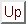

Next: プログラムの整理
Previous: 全運動量を0にする
前回までのプログラムにより、全運動量のゼロ化が実現された。続いて、その速度から計算される温度  運動エネルギーを設定してみよう。N個の粒子が2次元の格子内で運動する場合、粒子のもつ運動エネルギーと系の温度Tには次の関係が成り立つ。
運動エネルギーを設定してみよう。N個の粒子が2次元の格子内で運動する場合、粒子のもつ運動エネルギーと系の温度Tには次の関係が成り立つ。
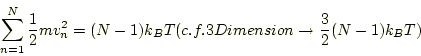 |
(2) |
ここに(N-1)は全運動量がゼロになるという拘束条件が各方向に存在するため自由度が1減ることを意味する。簡略化のため、引き続き質量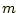 は1とする。また、温度
は1とする。また、温度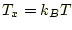 をある値(例えば
をある値(例えば
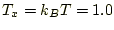 )に設定するためには、現在の粒子の速度を用いて計算される次のファクター
)に設定するためには、現在の粒子の速度を用いて計算される次のファクター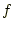 を速度に掛け更新することによって行われる。
を速度に掛け更新することによって行われる。
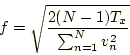 |
(3) |
この部分を前回のプログラムに追加し、得られた結果をgnuplotのベクトル表示を利用して再度確認すること。


Next: プログラムの整理
Previous: 全運動量を0にする
Hitoshi Takamura
平成16年12月26日